The Z Test for a Population Mean Requires That You Know the Value of

Hypothesis Testing: Z-Scores

A guide to understanding what hypothesis testing is and how to translate and implement the z-test

Effigy i. Two-tailed & One-tailed exam | Epitome by writer

Surely in some part of your training or fifty-fifty in your piece of work, y'all have heard about hypothesis tests, but practice you know what they are for or how they are implemented? If the respond is no, I invite y'all to stay because nosotros volition talk about the famous hypothesis tests in this blog.

Get comfortable, go get your favorite drink and enjoy.

Hypothesis Tests

Imagine that in an commodity we read the statement: "… all adults on average slumber 7 hours a twenty-four hours". How to validate that the previous assertion is valid? With hypothesis tests.

Hypothesis tests allow us to validate some belongings that is assumed from a population concerning the property extracted from a representative sample. From our previous case, "all adults" is our population, from which we would seek to validate the property that refers to "sleep 7 hours a day".

To validate the claim that all adults sleep vii hours a mean solar day, we would need to collect a meaning sample to be compared with the population.

Imagine that nosotros ask 100 random adults how many hours they sleep a day, from which we obtain that on boilerplate they sleep 7.5 hours a day. And then, our sample mean is 7.five hours which is 0.5 college than the population mean.

So given the sample mean, we may think: since the difference is but 0.v, practice we assume that the claim is right? or since it was not the aforementioned, do we say that the claim is incorrect? Well, to solve these questions we would demand to employ something chosenz-scores which nosotros will see in particular later.

Everything is elementary so far right? earlier standing, let'south formalize a few things.

To perform a hypothesis examination, we need to determine ii hypotheses: the null hypothesis (or H0 ) and the alternative hypothesis (or H1 ). The null hypothesis refers to the formalization of the assertion of a statistical belongings of the population to be verified. The alternative hypothesis is the antagonist of the null hypothesis, that is, it is the assertion that refutes the null hypothesis.

Now let'southward get back to the previous problem, how to know if the population argument is correct when our sample hateful turned out to be 0.5 higher? To address this question, nosotros first need to know a few more things.

To check if the statement in the nil hypothesis is correct, nosotros need to define a significance level. Ordinarily, the significance level is 5% and is interpreted equally follows: if the probability of our sample mean is less than or equal to v%, and so the zilch hypothesis is rejected, on the other hand, if the probability of our sample mean is greater than 5%, then the cypher hypothesis remains or fails to be rejected.

But why 5%? Let'southward proceed to understand how this works.

When working with a normal distribution, for practicality, such distribution is normally transformed to a standard normal distribution, this procedure is called standardization. The standard normal distribution is a symmetric curve with a mean of 0 and a standard difference of 1 whose area nether the curve is 1 or 100% (every bit shown in figure 2). This standardization allows us to quantify the number of standard deviations at which a sample hateful is found concerning the population mean. The number of standard deviations is determined by the z-scores. Smash!

Effigy 2. Standard Normal Distribution | Epitome by writer

So, since we work with a standard normal distribution, all the values of the sample hateful apropos the population mean are normally distributed, therefore, at least 95% of all the sample ways fall within two standard deviations of the population mean, that is, there is less than 5% probability of obtaining a sample hateful beyond 2 standard deviations of the population hateful.

Figure iii. Two-tailed test with alpha = 5% | Image by writer

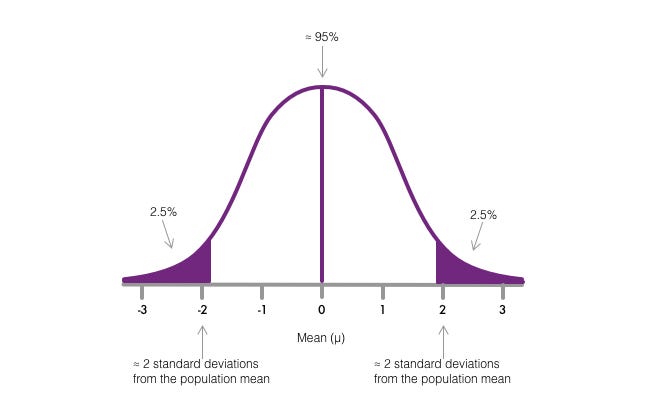
Before standing, allow's formalize a few things:

The null hypothesis is rejected when the sample hateful is associated with a depression probability of occurrence. The null hypothesis is retained when the sample mean is associated with a high probability of occurrence.

Such probability of occurrence is meliorate known equally p-value.

So, if the probability of occurrence (or p-value) is less than or equal to v%, the cypher hypothesis is rejected, on the other hand, if the probability of occurrence (or p-value) is greater than 5%, the null hypothesis is retained.

In summary, the hypothesis testing methodology is described every bit the sequence of the post-obit steps:

1. Land the hypothesis: In this phase, the statement to be tested is declared, that is, the null hypothesis. Consequently, the alternative hypothesis is generated. The alternative hypothesis tin determine three types of cases: that the population mean is greater than (>), less than (<), or not equal (≠) to the value defined in the null hypothesis.
2. Gear up the criteria for a decision: The criterion for the decision is defined through the level of significance, normally defined at five%, nonetheless, 10% and one% are also unremarkably used.
3. Compute de test statistic: In this phase, the statistical test is applied to determine how close or far our sample mean is concerning the population mean. There are several statistical tests for different types of distributions, usually, for a normal distribution, the z-test or test based on z-scores is used.
4. Make a decision: Given the result obtained past the statistical test and the criteria for the decision divers in step 2, whether the null hypothesis is rejected or retained is determined.

Awesome, now that we understand what a hypothesis test is and the intuition about the implementation with some formalities, now permit's see how to apply the z-test for each of the variants that the alternative hypothesis could accept, let'southward go to the next section!

Directional & Non-directional Hypothesis Tests

Depending on what nosotros know about the population, it is the exam that nosotros can apply. If we know the mean and the variance, the z-examination would exist the about appropriate choice.

Equally nosotros saw in the previous section, the culling hypothesis is the one that refutes or contradicts the null hypothesis. This contradiction refers to the fact that the sample mean is greater than (>), less than (<), or different (≠) from that established in the nil hypothesis, that is, the alternative hypothesis can be directional or non-directional.

Figure 4. Directional and non-directional tests | Prototype by author

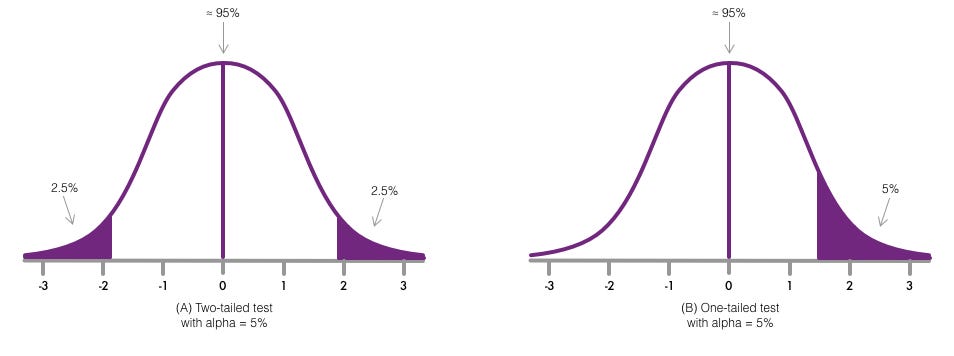
The hypothesis is directional when the alternative hypothesis defines an orientation, either greater than (>) or less than (<) that established in the null hypothesis. For example:

• Null hypothesis: All adults slumber vii hours a solar day
• Alternative hypothesis: All adults sleep more than 7 hours a day

In the same way, the hypothesis tin be oriented as follows:

• Null hypothesis: All adults slumber 7 hours a day
• Alternative hypothesis: All adults sleep less than 7 hours a 24-hour interval

In both cases, the hypothesis is directional.

On the other paw, the hypothesis is non-directional when the alternative hypothesis does not define an orientation explicitly, that is, it simply determines that the hypothesis is different from the null hypothesis. For instance:

• Null hypothesis: All adults slumber vii hours a twenty-four hours
• Alternative hypothesis: All adults do non sleep seven hours a day

Peachy, now that we know what hypothesis testing is when to apply the z-test, and the orientations of the hypotheses according to the culling hypothesis, information technology'southward time to see a couple of examples. Let's go for it!

Example

Let's take the post-obit argument: "In a study, it was establish that all adults slumber 7 hours a mean solar day with a standard difference of one hour. Suppose we accept a sample from which we obtain a sample mean of viii hours. Perform a hypothesis test to verify the population mean"

To perform the hypothesis test, we follow the following iv steps:

Step 1: State the hypothesis. Imagine that we want to accost a non-directional hypothesis, our null hypothesis and culling hypothesis would be as follows:

• Goose egg hypothesis: Adults sleep 7 hours a twenty-four hour period
• Alternative hypothesis: Adults do not sleep 7 hours a day

Step 2: Set up the criteria for a decision.

The level of significance will be 0.five or 5%, which consequently determines blastoff = 0.5. Since we are addressing a nondirectional two-tailed test, we dissever the alpha value in one-half and then that an equal proportion of the area is placed in the upper and lower tail, as shown in Figure 3. The calculation of alpha is shown in equation 1.

Equation 1. Processing blastoff for a 2-tailed exam

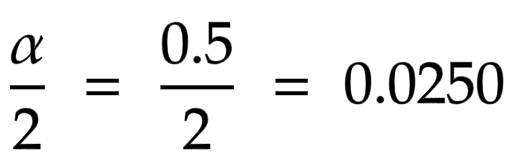
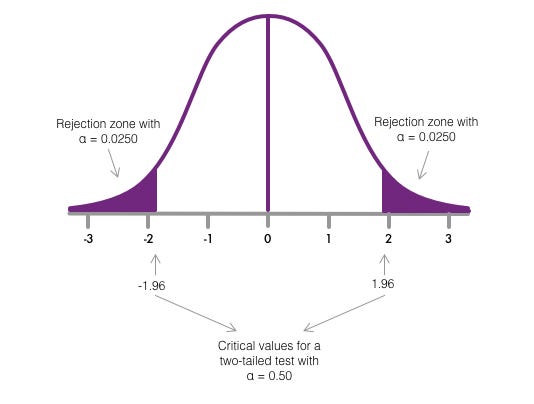
Since we accept calculated the alpha value for a 2-tailed test, then we can decide the critical values, that is, those values that decide the rejection zone in the standard normal distribution.

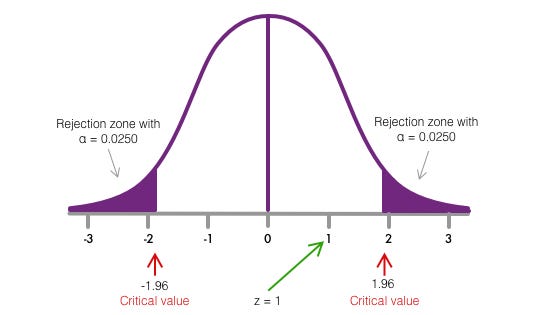
To notice the critical values, we look at z-table the value of z that approximates an expanse under the curve similar to 0.0250. In this example, the value is 1.96, that is, if the value of our statistical test is greater than ane.96 standard deviations or less than -1.96 standard deviations, nosotros would exist in the rejection zone.

Effigy five. Rejection zone for alpha = 0.five | Image past writer

Pace 3: Compute the test statistic. In one case we accept defined the hypotheses also every bit the level of significance, we proceed to calculate z statistic.

The z statistic gives united states the number of standard deviations that a sample mean deviates from the population mean in a standard normal distribution. The z statistic is calculated by taking the sample mean minus the population mean (defined in the nothing hypothesis), divided by the standard deviation, as shown in equation 2.

Equation two. Z statistic calculation

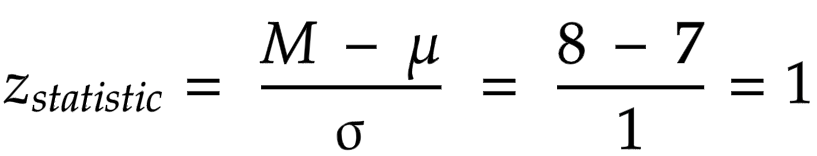
Then, from the calculations, nosotros obtain that z = i . Finally, we must brand the decision, which we will practice in the next pace.

Pace 4. Make a conclusion. To make a conclusion, nosotros look at the critical value obtained in footstep 2 based on the level of significance. Since the value of the z statistic(obtained in step iii) is less than the critical value, it is decided to keep the null hypothesis.

Effigy half-dozen. Z-score = one | Image by author

Finally, the probability of obtaining z = one is determined by p-value . To find such value, we use the unit of measurement normal table. In this case, we are looking for the z-score equal to 1, the value is 0.15866. Given that we address an alternative ii-tailed hypothesis, we multiply the obtained value by 2, leaving p = (0.15866) * 2 = 0.31732.

In step 2 nosotros determine the level of significance equal to v%, that is, if the p-value is less than 5%, the hypothesis is rejected, otherwise, if the p-value is greater than v%, the hypothesis goose egg remains. In this case, p = 31.7%, beingness greater than 5%, therefore the aught hypothesis is maintained.

References

[1] Introduction to Hypothesis Testing

mcknightsucan1991.blogspot.com

Source: https://towardsdatascience.com/hypothesis-testing-z-scores-337fb06e26ab

Share this post